일반적으로 가중치가 크면 과적합이 발생한다고 알려져 있다.
그래서 가중치의 크기를 규제하는 방법으로 L1-regularization, L2-regularization을 활용하곤 한다.
(가중치 규제와 관련된 포스팅은 이 링크를 참고)
https://ohsy0512.tistory.com/31
그러면 왜 가중치의 크기가 클 때 과적합이 발생할까?
이 주제에 대해서 한국어 자료부터 영어 자료까지 찾아봤지만 자세히 설명된 포스팅이 없었다.
그래서 나름 혼자 고민하면서 이해한 바를 설명해보려 한다.
다음의 예시를 보자.

$x1$과 $x2$라는 feature가 있을 때, $x = x1 + x2$ 혹은 $x = 10x1 + 10x2$에 대하여 sigmoid(x)를 적용한 결과다.
두 그래프의 차이는 weight의 크기이다.
왼쪽에 비해 오른쪽은 단순히 weight의 크기가 10배로 늘어났지만 경사하강법의 관점에서는 매우 큰 차이가 있다.
- 왼쪽 그래프: $x = 0$ 주위로 완만한 gradient를 가진다. x값이 커지거나 작아질수록 gradient가 완만하게 0에 가까워진다.
- 오른쪽 그래프: $x = 0$ 주위로 급격한 gradient를 가진다. x값이 커지거나 작아질수록 gradient가 급격하게 0에 가까워진다.
- 모델이 좋은 학습을 하기 위해서는 그래프 중간의 gradient 값을 통해 점진적으로 가중치를 업데이트 해야 한다.
- 하지만 오른쪽 그래프는 중앙의 linear한 gradient가 훨씬 짧고 양끝이 0으로 급격하게 수렴하는 형태이다. 그래서 가중치를 점진적으로 갱신하지 못하고 지나치게 빨리 변하거나 거의 갱신하지 못하게 된다. 즉, 입력 데이터의 작은 변화에도 민감한 모델이 된다.
이는 실제로 코드로 확인해볼 수 있다.

- sigmoid: sigmoid의 함숫값을 구해주는 함수
- dev_sigmoid: sigmoid의 미분값(gradient)를 구해주는 함수
우선 weight가 크지 않을 때, 입력 데이터 간의 차이가 크지 않은 경우이다.
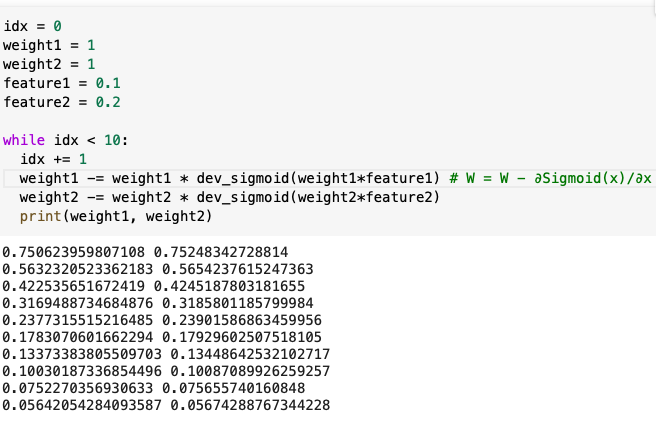
- weight1 = 1, weight2 = 1
- feature1 = 0.1, feature2 = 0.2
weight1과 weight2 모두 1에서 시작하여 정상적으로 학습이 진행되는 것을 확인할 수 있다.
이번에는 weight가 크지 않을 때, 입력 데이터 간의 차이가 큰 경우이다.

- weight1 = 1, weight2 = 1
- feature1 = 0.1, feature2 = 0.5
이번에도 weight1과 weight2 모두 1에서 시작하여 정상적으로 학습이 진행되었다.
반면 weight가 클 때, 입력 데이터 간의 차이가 크지 않은 경우를 보자.

- weight1 = 10, weight2 = 10
- feature1 = 0.1, feature2 = 0.2
점진적으로 gradient가 감소하는 것을 확인할 수 있다.
마지막으로 weight가 클 때, 입력 데이터 간의 차이가 큰 경우를 보자.

- weight1 = 10, weight2 = 10
- feature1 = 0.1, feature2 = 0.5
weight1은 정상적으로 경사하강법을 진행하고 있다.
문제는 weight2이다.
가중치가 9.xxx에서 갱신되지 않고 계속 유지되고 있다. feature1과 feature2는 분포에서 아무런 차이가 없고 단지 5가 곱해져 있을 뿐인데도 말이다...!
직관적으로 예를 들면 키가 0.1이고 몸무게가 0.5인 사람이 10명이 있다고 하자.
이 때 feature간 스케일만 다를 뿐 전체 데이터의 분포는 똑같은데도,
이 모델에서는 키의 최종 가중치가 0.68, 몸무게의 최종 가중치가 9.24로 몸무게가 decision에 훨씬 중요한 변수라고 인식하고 있는 것이다.
즉 가중치가 클 수록 입력값의 작은 변화에도 민감해지게 되고, 입력 데이터에 섞여 있는 noise나 scale에 민감해지게 된다.
그래서 train data에 섞여 있는 noise나 outlier까지도 모조리 학습하게 되고, 과적합(overfitting)을 유발한다.
'AI > ML DL' 카테고리의 다른 글
| 가중치 규제(Weight Regularization) (0) | 2023.03.19 |
|---|