행렬
행렬은 벡터를 원소로 가지는 2차원 배열이다.

행렬은 행과 열을 갖는다.

1. 행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱
행렬끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱, 스칼라곱을 계산할 수 있다.
벡터와 마찬가지로 각 인덱스 위치끼리 연산하면 된다.
2. 행렬 곱셈
행렬 곱셈은 앞 행렬의 열과 뒤 행렬의 행의 수가 같아야 한다.

만약 $X_{mn}$와 $Y_{nl}$을 곱하면 결과는 m행과 l열로 구성된 행렬이 된다.
연산 결과가 이렇게 나타나는 이유는 행렬곱이 내적을 통한 연산이기 때문이다.
즉 행렬의 각 원소는 앞 행렬의 i번째 행벡터와 뒤 행렬의 j번째 열벡터를 내적한 결과로 구성되며, 곱의 순서에 따라 값이 달라지므로 앞 행렬과 뒤 행렬의 순서를 바꿀 수 없다.

3. 행렬을 이해하는 방법
벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타낸다.
행렬의 행벡터 $x_i$는 i번째 데이터를 의미한다.
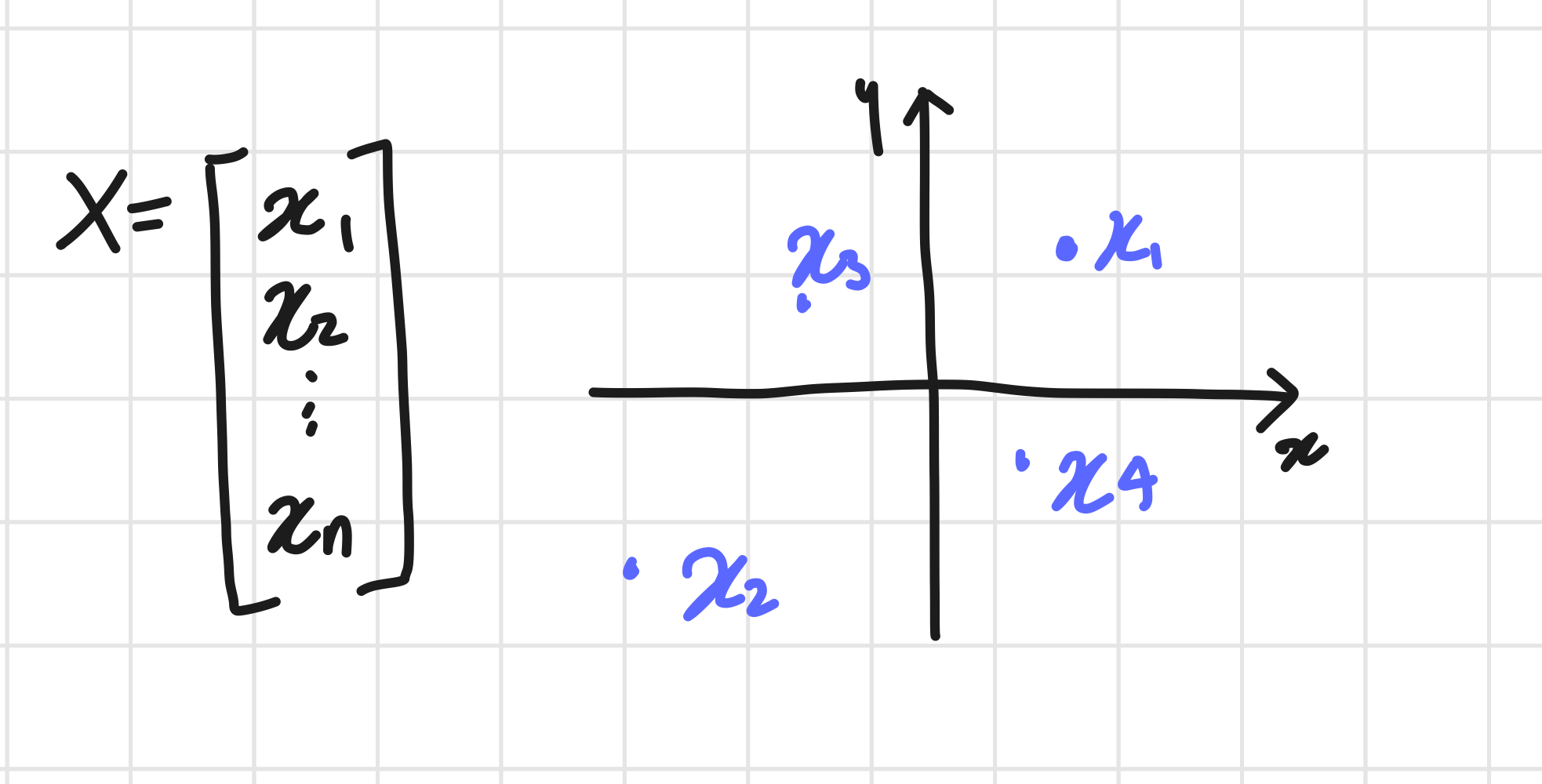
행렬의 원소 $x_ij$는 i번째 데이터의 j번째 변수의 값을 말한다.
이걸 기계학습에 적용하여 설명할 수 있다. 예를 들어, n 명이 m 개의 feature에 대한 데이터가 있다고 했을 때, $x_ij는$ i번째 사용자의 j번째 feature의 값을 의미하게 되는 것이다.
또 행렬은 벡터공간에서 사용되는 연산자로 이용할 수 있다.
행렬곱을 통해 벡터를 다른 차원의 공간으로 보내는 것이다.

행렬곱을 통해 기계학습에서 패턴을 추출할 수 있고 데이터를 압축할 수도 있다.
4. 역행렬
항등행렬은 대각선의 원소만 1이고 나머지는 전부 0인 행렬을 가리킨다.
역행렬은 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 의미하고 $A^{-1}$로 표기한다.
역행렬은 행과 열의 개수가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
만약 역행렬을 계산할 수 없다면 유사역행렬 또는 무어 펜로즈 역행렬을 이용한다.
무어펜로즈 역행렬은 $A^{+}$로 표기한다.

'Naver Boostcamp' 카테고리의 다른 글
| [Pytorch 기본]nn.Module (0) | 2023.03.14 |
|---|---|
| [AI Math] 경사하강법 (0) | 2023.03.12 |
| [AI Math] 벡터 (0) | 2023.03.09 |
| [Python] 객체 지향 프로그래밍, Numpy, Pandas (0) | 2023.03.07 |
| [네이버 부스트캠프 AI Tech 5기] 온보딩 키트 / 주간 학습 일정 (1) | 2023.03.06 |